| HOME | HELP | FEEDBACK | SUBSCRIPTIONS | ARCHIVE | SEARCH | TABLE OF CONTENTS |
Corresponding author: Leonard G. Robbins, Università di Siena, Via P. A. Mattioli 4, 53100 Siena, Italy., robbins{at}unisi.it (E-mail)
| ABSTRACT |
|---|
Graduate school programs in genetics have become so full that courses in statistics have often been eliminated. In addition, typical introductory statistics courses for the "statistics user" rather than the nascent statistician are laden with methods for analysis of measured variables while genetic data are most often discrete numbers. These courses are often seen by students and genetics professors alike as largely irrelevant cookbook courses. The powerful methods of likelihood analysis, although commonly employed in human genetics, are much less often used in other areas of genetics, even though current computational tools make this approach readily accessible. This article introduces the MLIKELY.PAS computer program and the logic of do-it-yourself maximum-likelihood statistics. The program itself, course materials, and expanded discussions of some examples that are only summarized here are available at http://www.unisi.it/ricerca/dip/bio_evol/sitomlikely/mlikely.html.
AS most of us still impress on our introductory genetics students,
genetics started with the counting of offspring produced by
crosses. Although many of us now spend a large fraction of our
time at a chemical bench, crosses, and the discrete data they
generate, still remain a core tool in our work. Remarkably, the
early synergism between genetics and statistics is now mostly absent
from the pages of this journal. Virtually all of us are familiar with
log of odds (LOD) score analysis of human genetic data, and most of
us can do a  2 test
against a priori expectations or a
2 test
against a priori expectations or a  2
contingency test. Nevertheless, in most articles in GENETICS that contain cross data there is either no
statistical analysis at all or transformation of the discrete data to
frequencies—accompanied by confidence intervals and statistics, if
any, that were originally devised for dealing with continuous
variables. The questions we are actually interested in asking go well
beyond the few methods of discrete-data analysis we've learned, so we
either rely on an eye-ball approach or fall back on the
continuous-variable methods taught in the usual statistics courses.
Given the loss of power and plethora of mathematical and inferential
pitfalls that the latter entails, the eyeball may often be the
better instrument.
2
contingency test. Nevertheless, in most articles in GENETICS that contain cross data there is either no
statistical analysis at all or transformation of the discrete data to
frequencies—accompanied by confidence intervals and statistics, if
any, that were originally devised for dealing with continuous
variables. The questions we are actually interested in asking go well
beyond the few methods of discrete-data analysis we've learned, so we
either rely on an eye-ball approach or fall back on the
continuous-variable methods taught in the usual statistics courses.
Given the loss of power and plethora of mathematical and inferential
pitfalls that the latter entails, the eyeball may often be the
better instrument.
This need not be the case, and in many areas of research this is
not the case. Areas as diverse as animal behavior, clinical trials,
and signal and image processing are replete with powerful examples of
discrete analysis. (The CCAR database, for example, contains nearly
3000 entries for "maximum-likelihood" for the 3 years 1993–1995.)
There are, of course, examples in genetics as well: LOD scores (see
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 2 = 8.07,
1 d.f., P ~ 0.004) included any statistical analysis at all.
Obviously, statistical tests may not have been needed in these
articles; simple perusal of percentages can often be convincing.
Nevertheless, methods for analysis of discrete data are available,
their use is not difficult, and they can be revealing. They can also
help us avoid designing complicated crosses that cannot, in the end,
be analyzed.
2 = 8.07,
1 d.f., P ~ 0.004) included any statistical analysis at all.
Obviously, statistical tests may not have been needed in these
articles; simple perusal of percentages can often be convincing.
Nevertheless, methods for analysis of discrete data are available,
their use is not difficult, and they can be revealing. They can also
help us avoid designing complicated crosses that cannot, in the end,
be analyzed.
Methods for discrete analysis have been a step-sister in statistics,
but discrete multivariate analysis, with a thorough exegesis in
![]()
![]()
The value of a multivariate mode of thinking is well illustrated
by the erroneous presentation of the a priori  2 test in
a popular introductory genetics textbook (
2 test in
a popular introductory genetics textbook (![]()
![]()
![]()
 2 =
5.2, 3 d.f., P = 0.156), but done correctly there is, in fact, a
significant indication of linkage (
2 =
5.2, 3 d.f., P = 0.156), but done correctly there is, in fact, a
significant indication of linkage ( 2 = 5.0,
1 d.f., P = 0.025), while there are no significant differences (for
example, there are no significant marker viability effects) in
recovery of reciprocal products (
2 = 5.0,
1 d.f., P = 0.025), while there are no significant differences (for
example, there are no significant marker viability effects) in
recovery of reciprocal products ( 2 =
0.202, 2 d.f., P = 0.904). In the new book, a contingency test of
statistically independent recovery of the allelic combinations, in
place of the a priori test for Mendelian independent
assortment, yields a result (
2 =
0.202, 2 d.f., P = 0.904). In the new book, a contingency test of
statistically independent recovery of the allelic combinations, in
place of the a priori test for Mendelian independent
assortment, yields a result ( 2 =
5.02, 1 d.f., P = 0.025) very close to that of the simpler test
for deviation from a 1:1 ratio of parental:nonparental.
2 =
5.02, 1 d.f., P = 0.025) very close to that of the simpler test
for deviation from a 1:1 ratio of parental:nonparental.
The foregoing example does not illustrate a need for analysis of
maximum likelihood, nor even for the contingency test used in
![]()
 2 test
would have been adequate. It does, however, illustrate how failing to
separate different biological processes can lead one astray. Testing
for linkage, a recombination fraction under 50%, is not the same as
testing for all possible distortions of genotype frequencies.
2 test
would have been adequate. It does, however, illustrate how failing to
separate different biological processes can lead one astray. Testing
for linkage, a recombination fraction under 50%, is not the same as
testing for all possible distortions of genotype frequencies.
Not every problem in formal genetics can be resolved just with
clear thinking and  2 tests.
The advent of powerful personal computers, however, makes the methods
that are needed accessible to those who, like myself, are neither
mathematicians, statisticians, nor professional programmers. Several
of the most common questions geneticists must contend with can be
asked: What are the best estimates of genetic parameters? Does a
hypothesis adequately account for the observed effects? How can we
test whether an experiment and control respond differently to a
variable we're interested in, when both the experiment and control
are also affected by some other variable? Is there significant
variation in what we're scoring? Is there a correlation between two
variables? How important is the correlation? Moreover, with use of
the computer allowing us to strip away much of the mathematical
complexity, the major task left for the geneticist is the clear
definition of the question(s) to be asked.
2 tests.
The advent of powerful personal computers, however, makes the methods
that are needed accessible to those who, like myself, are neither
mathematicians, statisticians, nor professional programmers. Several
of the most common questions geneticists must contend with can be
asked: What are the best estimates of genetic parameters? Does a
hypothesis adequately account for the observed effects? How can we
test whether an experiment and control respond differently to a
variable we're interested in, when both the experiment and control
are also affected by some other variable? Is there significant
variation in what we're scoring? Is there a correlation between two
variables? How important is the correlation? Moreover, with use of
the computer allowing us to strip away much of the mathematical
complexity, the major task left for the geneticist is the clear
definition of the question(s) to be asked.
With the hope of creating an enhanced awareness of these methods among the next generation of geneticists, a set of real-world examples and a program for numerical approximation of maximum likelihoods were used as the core of a graduate-level course offered first in 1996 at Michigan State University and again in 1998 at the University of Siena. The course presented a guide to this mode of analysis by means of examples, some already published and some new. In each case, I chose actual experiments rather than invented examples. For some of the examples, the genetics is nontrivial and the explanation of the crosses is lengthy, but this allows the student or reader to judge the value and difficulty of applying this method to real-world situations. The examples are as follows: (1) mapping a dominant of reduced penetrance; (2) testing for a correlation between two chromosome-behavior phenotypes; (3) testing whether a meiotic mutant affects chiasma interference; and (4) testing for the effects of a gene on viability in the presence of confounding variables. The first two examples are covered here, while the latter two are only briefly described with the full discussions included at the web site.
| BASIC METHODOLOGY |
|---|
Maximum-likelihood estimates and hypothesis testing:
In
the following sections, computer-assisted techniques for estimating
parameters (such as map distances), testing for goodness-of-fit, and
comparing hypotheses are described. All of them are based on the
method of maximum likelihood (![]()
![]()
Suppose that the probability of getting an offspring of a given
class is p and that N of these offspring were observed in
an experiment. The likelihood of getting those N offspring is
defined as: L = pN. Crosses yield multiple offspring
classes, each with its own probability, but, because different
offspring are independently produced, the likelihood for the entire
experiment is the product of the likelihoods. For example,1 a
test cross involving two genes that are 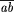 map units
apart yields CO crossover offspring and NCO noncrossover offspring,
and the likelihood is L =
map units
apart yields CO crossover offspring and NCO noncrossover offspring,
and the likelihood is L = 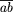 CO (1 -
CO (1 - 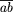 )NCO. The value of
)NCO. The value of 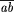 that
maximizes L is the estimate of
that
maximizes L is the estimate of 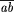 that we use;
in this case it is CO/(NCO + CO). If we were dealing with a more
complex situation where there are many parameters, we would want to
find the values of all of the parameters that simultaneously maximize
L. Noting that as a number increases, its logarithm increases
as well, we can, with the same effect and usually more easily, find
the parameter values that maximize the logarithm of L. In the
following, the maximum values of these functions are denoted
that we use;
in this case it is CO/(NCO + CO). If we were dealing with a more
complex situation where there are many parameters, we would want to
find the values of all of the parameters that simultaneously maximize
L. Noting that as a number increases, its logarithm increases
as well, we can, with the same effect and usually more easily, find
the parameter values that maximize the logarithm of L. In the
following, the maximum values of these functions are denoted 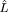 and ln
and ln
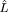 .
.
Most of the time we are not only interested in estimating the parameters, but in testing whether a hypothesis provides a sufficient explanation for the experimental variation or in testing whether there are significant differences between two (or more) hypotheses. For example, if we suspect a correlation between two variables, we would want to test three things. First, we need to test whether there is significant variation in these parameters in the first place. That is, does a hypothesis of no variation in one or the other parameter fail a goodness-of-fit test? Second, we will want to know whether a model that includes a correlation with slope other than zero is significantly better than the hypothesis of no variation (equivalent to a correlation with slope = 0). That is, we must compare two hypotheses. Third, we will want to know how much of the variation is explained by the correlation, i.e., its sufficiency; another goodness-of-fit test.
In many cases, the obvious test for goodness-of-fit is a straightforward
 2. That
is, we use the maximum-likelihood estimates of the parameters to find
the probabilities of each class, multiply these probabilities by the
appropriate total(s) to get expected numbers, and calculate
2. That
is, we use the maximum-likelihood estimates of the parameters to find
the probabilities of each class, multiply these probabilities by the
appropriate total(s) to get expected numbers, and calculate  2 as a
measure of the difference between observations and expectations. The
degrees of freedom are then the number of independent observations
less the number of parameters estimated from the data.
2 as a
measure of the difference between observations and expectations. The
degrees of freedom are then the number of independent observations
less the number of parameters estimated from the data.
When we wish to compare two hypotheses, H1 and H2, however, a
different measure is often more appropriate or more convenient. This
is the G (also known as G2) statistic (![]()
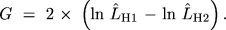
G is distributed approximately as  2 with
degrees of freedom equal to the difference between the numbers of
parameters of the two hypotheses. The approximation to
2 with
degrees of freedom equal to the difference between the numbers of
parameters of the two hypotheses. The approximation to  2 is
asymptotic and becomes more exact as sample size increases.
2 is
asymptotic and becomes more exact as sample size increases.
Note that in many cases a test for sufficiency, usually stated as
a test for goodness-of-fit, can also be described as a comparison of
two hypotheses. For example, if H1 includes m parameters
(unknowns to be solved for) and there are m independent
observations (knowns), and the parameters can take any numerical
value, the maximum-likelihood estimates of the parameters are
identical to what would be obtained by solving m equations in
m unknowns. Because H1 merely describes all of the variation,
there is no test for its sufficiency (aside from the possibility of
getting utterly absurd parameter values) and calculating  2 will
yield a value of 0. A comparison of another hypothesis, H2, to
H1 by a G test is then logically equivalent to testing H2 for
goodness-of-fit. The values of G for H2 vs. H1 and the
2 will
yield a value of 0. A comparison of another hypothesis, H2, to
H1 by a G test is then logically equivalent to testing H2 for
goodness-of-fit. The values of G for H2 vs. H1 and the
 2 for
goodness-of-fit of H2 will generally be the same, or very nearly so.
For such tests, the choice of whether it is done as a
2 for
goodness-of-fit of H2 will generally be the same, or very nearly so.
For such tests, the choice of whether it is done as a  2 or
G test is largely a matter of convenience (if, for example,
the values of ln
2 or
G test is largely a matter of convenience (if, for example,
the values of ln 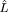 H1 and ln
H1 and ln 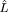 H2 have already been found), esthetics, or habit.
H2 have already been found), esthetics, or habit.
How can we find the parameter values that maximize ln L? For
pedigree data, in years past we would have gone to MORTON's (1955) tables, but we would now most likely
use one of the readily available LOD score computer programs
(![]()
The MLIKELY.PAS program:
MLIKELY.PAS is a Pascal program
that, in its current version, is compiled under TURBO PASCAL 4.0
(Borland Intl.). It is not user friendly—it lacks a graphical user
interface, does not support a mouse, and requires that the user
convert a few equations into Pascal syntax and paste them into the
program, which then must be compiled and run. It is, however,
geneticist friendly. It can work with virtually any set of crosses,
whether simple or complex. The expressions the user needs to write
are most often direct translations of a Punnett square or logic
tree. And running the program requires only answering a series
of questions and entering the data. The heuristic used is brutally
simple; the user provides first guesses of the parameter values
or accepts the program's defaults, and the computer increases
and decreases those values, moving sequentially through the
list of parameters using ever smaller intervals, until it finds
the maximum of ln L to whatever precision is desired. A few
tricks are used to speed operation:
Although incorporated piecemeal in MLIKELY.PAS either intuitively or empirically, these procedures are not uncommon in optimization algorithms, and constraining parameter ranges is similar to the use of "hints" in speeding artificial intelligence schemes. MLIKELY.PAS provides output in a variety of formats: screen-readable, printable, and word-processor and spreadsheet importable, and saves the data in a reusable file so that they need be entered only once.
There are algorithms that can find a maximum more quickly. For example, the "optimizer" found in the QUATTRO PRO (Corel) spreadsheet package can estimate the derivatives first to speed the search for a maximum. MLIKELY.PAS is not, in any case, unreasonably slow. Iteration times are indicated in the examples that follow, in each case for runs on a 80486/33 computer with each parameter estimated to a precision of better than 1 part in 108. Even with a less-than-state-of-the-art PC, the running time is most often far less than the thinking time needed to define the problem in the first place.
The simple heuristic used in MLIKELY.PAS can cause two problems that the user should be aware of. First, because the parameters are handled sequentially, if two or more of the starting guesses are impossible, i.e., if they give negative expected frequencies, the program will not find the maximum, but will issue a warning message. Starting with more reasonable guesses is the cure for this problem. Second, a likelihood function may have more than one peak. As with other iterative peak-finding procedures, once in the neighborhood of a peak, even if it is not the highest in the entire landscape, the program may halt at that local maximum. It is even possible to have a model so badly structured that ln L is an oscillating function, such as a sine wave, but this is unlikely in any genetics application. A program designed to find likelihoods for only one class of problem can usually be rigged to avoid this. In contrast, although MLIKELY.PAS can be fooled by local maxima, and is not usable for every type of application to which maximum likelihood analysis applies, it can accommodate any model for which one can write the probabilities of getting each observed class.
That multiple peaks in an iterative process can be dangerous has
certainly been seen in the study of human molecular evolution; the
primacy of a mitochondrial Eve, while appealing, was supported by a
maximum-parsimony tree that was not unique (![]()
![]()
The generally good behavior of the iteration algorithm used in MLIKELY.PAS could be a result of mere luck, but has probably occurred because formal genetics problems, as opposed to problems in taxonomy, are often well structured even when they involve many parameters. For example, in describing recombination in several regions, there will be several single-crossover frequencies to be estimated, but all of them behave in an algebraically similar fashion.
The behavior of MLIKELY.PAS during the iteration process as well as its output can provide useful indications of potential problems. For example, in the second example of this report, which considers testing for correlation using discrete data, an example of the effect of improperly bounding a parameter's search space is considered. It is nevertheless good practice to start with several widely different sets of parameter guesses to check that you always end up at the same peak.
MLIKELY.PAS also calculates  2 for a
goodness-of-fit test of the hypothesis. The user must supply Pascal
statements defining the sum(s) by which to multiply the probabilities
to get expected numbers. For data from a single cross, this is simply
the sum of all observations and that variable is already
calculated by the program, but for a series of crosses the sum for
each cross must be specified. Because the
2 for a
goodness-of-fit test of the hypothesis. The user must supply Pascal
statements defining the sum(s) by which to multiply the probabilities
to get expected numbers. For data from a single cross, this is simply
the sum of all observations and that variable is already
calculated by the program, but for a series of crosses the sum for
each cross must be specified. Because the  2
calculation is included in MLIKELY, it is often more convenient to
use this test of goodness-of-fit rather than an equivalent G
test when only a single hypothesis is being tested; only a single set
of equations need be written. In contrast, the likelihood-ratio
approach of a contrast between the hypothesis of interest and a
foil that explains all of the variation requires writing (or
editing) two versions of the equations, compiling and running the
program twice, and then calculating G.
2
calculation is included in MLIKELY, it is often more convenient to
use this test of goodness-of-fit rather than an equivalent G
test when only a single hypothesis is being tested; only a single set
of equations need be written. In contrast, the likelihood-ratio
approach of a contrast between the hypothesis of interest and a
foil that explains all of the variation requires writing (or
editing) two versions of the equations, compiling and running the
program twice, and then calculating G.
Inclusion of these calculations in MLIKELY serves another purpose
as well; seeing that the sum of the expected numbers equals the
sum of the observed numbers. Moreover, examination of the listing of
the  2 values
of the individual cells gives a good check that the probabilities
have been sensibly defined and accurately entered.
2 values
of the individual cells gives a good check that the probabilities
have been sensibly defined and accurately entered.
This article includes only enough information about the structure and running of the program to permit understanding how it serves the geneticist. MLIKELY (including all source code), sample sets of equations and data, as well as documentation files are available at the web site. Downloading carries two conditions: (1) neither the program, nor any substantial part of the program, may be used for commercial purposes nor incorporated into another program without my written permission; and (2) any improvements made, or versions modified for other Pascal compilers, will be shared with me so that they can be incorporated in future releases.
| EXAMPLES |
|---|
Parameter estimation—mapping a mutant of reduced
penetrance:
The top of Fig 1
illustrates a mouse genetics problem recently faced by J. Asher.
[This question arose in work following from ![]()
|
Starting with some wild guesses (d1 = 0.1, d2 = 0.1, C
= 0.1, and P = 0.99), in less than a second, the program finds
the values of the two distances, the coefficient of coincidence,
and the penetrance that maximize the ln likelihood of getting
the observed results (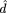 1
= 0.00634,
1
= 0.00634, 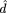 2 = 0.0525,
2 = 0.0525, 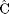 = 0.0, and
= 0.0, and 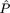 =
0.6605) and indicates, by the nonsignificant value of
=
0.6605) and indicates, by the nonsignificant value of  2 =
3.547 (3 d.f., P = 0.315), that this model provides a sufficient
description of the data.
2 =
3.547 (3 d.f., P = 0.315), that this model provides a sufficient
description of the data.
We can also take this a step further and examine the precision of these estimates. For example, we may be most interested in distance d1, the short A to B interval. What is the largest, or smallest, estimate of this distance that is still consistent with the data? To do this2, we (1) set a series of fixed values for d1; (2) allow the program to find the values of the other parameters that maximize the likelihood; and then (3) compare the results with those for the maximum-likelihood estimate of d1, i.e., when d1 = 0.00634.
We can use MLIKELY.PAS for the first two steps by changing just
four lines of code, so that d1 is treated as a constant,
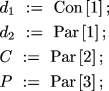
and repeating the iteration several times for different values of Con[1]. The data can be reentered, or the original data file may be modified in any text editor to change the number of parameters from 4 to 3 and the number of constants from 0 to 1.
We then need a statistic that allows us to compare the results. Two related comparisons are shown in Fig 2, one using the G statistic (Fig 2A) and the other using LOD scores (Fig 2B). MLIKELY.PAS does not itself calculate either G or LOD scores, but both of those statistics are easy to calculate and graph using a spreadsheet, and MLIKELY.PAS does provide a spreadsheet-importable (comma and space delimited) output file.
|
The values of the maximum ln L's were obtained with MLIKELY.PAS,
and a spreadsheet program (QUATTRO PRO; Corel) was used to find
G = 2 x [ln 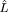 (d1
(d1
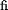 xed) - ln
xed) - ln
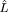 (d1 variable)] for each fixed value of
d1. These results are shown in Fig 2A. There
are four parameters when d1 is allowed to vary, and
three when it is fixed, giving 1 d.f., corresponding to P =
0.05 for G = 3.841 and P = 0.01 for G = 6.635.
Thus, the 95% upper bound for d1 is less than 3 map
units, and the 99% upper bound is less than 4 map units. The
probabilities provided by the G test correspond to those
conventionally used in most hypothesis testing; they are the
probabilities of getting a difference at least that large by
chance alone.
(d1 variable)] for each fixed value of
d1. These results are shown in Fig 2A. There
are four parameters when d1 is allowed to vary, and
three when it is fixed, giving 1 d.f., corresponding to P =
0.05 for G = 3.841 and P = 0.01 for G = 6.635.
Thus, the 95% upper bound for d1 is less than 3 map
units, and the 99% upper bound is less than 4 map units. The
probabilities provided by the G test correspond to those
conventionally used in most hypothesis testing; they are the
probabilities of getting a difference at least that large by
chance alone.
A different comparison, shown in Fig 2B, is often
used in human genetics. LOD (log of odds) scores are the
log10 of the ratio of the likelihoods under two
hypotheses, or, equivalently, the difference between the
log10 L's. The ln L output of MLIKELY.PAS
can be converted to base 10 by multiplying by ln10  2.30258,
and the LOD scores are found by subtraction. Note that the
conventions used in pedigree analysis, a LOD of +3 to demonstrate
linkage and -2 to exclude linkage, are substantially more
stringent than the usual critical values. This stringency is
reasonable when dealing with the tests of multiple hypotheses
implicit in using a progressive accumulation of families to decide
whether there is linkage, but is overkill for most cross data. It
is certainly overly stringent here, where we are already certain
that the genes are linked.
2.30258,
and the LOD scores are found by subtraction. Note that the
conventions used in pedigree analysis, a LOD of +3 to demonstrate
linkage and -2 to exclude linkage, are substantially more
stringent than the usual critical values. This stringency is
reasonable when dealing with the tests of multiple hypotheses
implicit in using a progressive accumulation of families to decide
whether there is linkage, but is overkill for most cross data. It
is certainly overly stringent here, where we are already certain
that the genes are linked.
Variation and correlation—the relationship between experimental
variables:
There are probably innumerable circumstances in which one
observes two or more variable phenotypes and wants to know whether
they are correlated. Where the phenotypes are metric, such as
bristle lengths in Drosophila, conventional regression analysis
can be appropriate, but regression analysis is also often used
for counted variables, such as crossovers and disjunctional
events, where a maximum-likelihood approach is more powerful and
more revealing. To illustrate this, some unpublished data from
my laboratory on the behavior of Rex are analyzed. The
results of similar analyses may also be found in ![]()
![]()
Rex is a repeated, heterochromatically located element of
Drosophila melanogaster. Acting maternally, it promotes
recombination between ribosomal-RNA gene arrays (rDNA) during early
embryonic mitoses (![]()
![]()
Those data came from crosses done along the way to mapping a
suppressor of Rex, a Su(Rex). At one point in this
process, a series of chromosomes that carried different segments of
the X chromosome were tested for suppression of Rex
activity. As this particular Su(Rex) turned out to be
autosomal, each genotype tested actually consisted of several flies
bearing the same X segment, but a random sampling of
Su(Rex) and non-Su(Rex) autosomes. The results of these
crosses are shown in Table 1.
Not only does the frequency of rDNA recombination appear to be
(and is) heterogeneous because of the different frequencies of the
Su(Rex) in the 10 samples, but the frequency of nondisjunction
varies as well. Are the two varying in a correlated fashion? We
can find out by comparing the values of ln 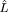 under
three hypotheses:
under
three hypotheses:
|
There are three G-test comparisons to be made:
The first step needed for making these comparisons is writing the probabilities of each of the progeny classes. Unfortunately, as illustrated in Fig 3, there are some complications caused by the actual cross used:
|
 ) and
therefore produce
) and
therefore produce  and
0 sperm, but the ratio of
and
0 sperm, but the ratio of  :0
sperm is not 1:1—
:0
sperm is not 1:1—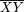 /0 males produce an excess of 0
sperm.
/0 males produce an excess of 0
sperm.
 embryos
resulting from normal disjunction. The exchange product
is an X/Y male (or gynandromorph), but if the
X carries the lethal, it too dies. Thus, to
completely describe each cross, we need parameters that
describe (i) the frequency of nondisjunction(n); (ii)
the frequency of Rex-induced exchange (r); and (iii)
the proportion of sperm that carry the
attached-XY (XY), and we must stay attentive
to the classes that die.
embryos
resulting from normal disjunction. The exchange product
is an X/Y male (or gynandromorph), but if the
X carries the lethal, it too dies. Thus, to
completely describe each cross, we need parameters that
describe (i) the frequency of nondisjunction(n); (ii)
the frequency of Rex-induced exchange (r); and (iii)
the proportion of sperm that carry the
attached-XY (XY), and we must stay attentive
to the classes that die.
The probabilities of the surviving genotypes among all zygotes are
then
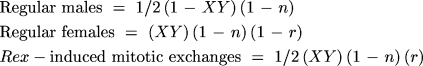
and
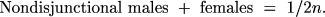
These are not, however, the probabilities of actually observing these offspring because we do not observe the lethals, which are 1/2(1 - XY)(1 - n) + 1/2(XY)(r)(1 - n) + 1/2n. To get the probabilities among survivors, we must divide the probability of each surviving genotype by the total probability of survival, 1 - 1/2(1 - XY)(1 - n) - 1/2(XY)(r) (1 - n) - 1/2n.
The equations needed to find the maximum-likelihood estimates of
the parameters under the three models and the iteration times to find
ln 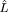 are shown in their Pascal incarnation in Fig 4.
Because only the parameter values change from cross to cross, a
single set of equations is contained within a loop. Only four lines
must be changed to accommodate each of the hypotheses.
are shown in their Pascal incarnation in Fig 4.
Because only the parameter values change from cross to cross, a
single set of equations is contained within a loop. Only four lines
must be changed to accommodate each of the hypotheses.
|
Each cross yields four offspring classes, three of which are
independent. Under H1, each cross is described by three separate
parameters so there is a unique solution for each. They are
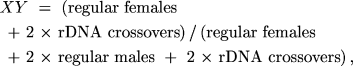
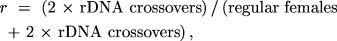
and
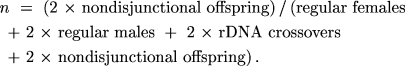
If each of the three parameters is a probability with values
between 0 and 1, MLIKELY.PAS must reach the same solutions, and
the goodness-of-fit  2 at the
end of the iteration process must be 0. Thus, even if the algebraic
solutions for XY, r, or n were not reasonably
obvious, MLIKELY.PAS would provide the solutions. In other words,
whenever the number of parameters equals the number of independent
observations, MLIKELY. PAS serves as a reasonably efficient equation
solver.
2 at the
end of the iteration process must be 0. Thus, even if the algebraic
solutions for XY, r, or n were not reasonably
obvious, MLIKELY.PAS would provide the solutions. In other words,
whenever the number of parameters equals the number of independent
observations, MLIKELY. PAS serves as a reasonably efficient equation
solver.
The algebraic solutions could turn out to be <0 or >1 either
because of sampling variation or because the three-probability
model is truly nonsensical. Were that the case, as long as the
parameters are constrained to the default 0–1 range, MLIKELY.PAS
would yield parameter estimates that do not match the calculated
values and we would get a positive  2 value.
Either discrepancy, algebraic solutions that are <0 or >1, or a
mismatch between the algebraic and numerical solutions, should
certainly clue the investigator to question the adequacy of the
model. For the data in Table 1, the
algebraic solutions for XY, r, and n are all in
the 0–1 range, running MLIKELY.PAS for H1 yields the same values, and
the
2 value.
Either discrepancy, algebraic solutions that are <0 or >1, or a
mismatch between the algebraic and numerical solutions, should
certainly clue the investigator to question the adequacy of the
model. For the data in Table 1, the
algebraic solutions for XY, r, and n are all in
the 0–1 range, running MLIKELY.PAS for H1 yields the same values, and
the  2 for H1
is 0. Note, however, that the proportion of
2 for H1
is 0. Note, however, that the proportion of  bearing
sperm is not actually involved in the hypotheses to be compared, and
it would have been legitimate to assume that the value of the
parameter XY was the same for all 10 crosses instead of
separately evaluating it for each cross. An appendix that considers
the pros and cons of different ways of formulating H1 is included at
the web site.
bearing
sperm is not actually involved in the hypotheses to be compared, and
it would have been legitimate to assume that the value of the
parameter XY was the same for all 10 crosses instead of
separately evaluating it for each cross. An appendix that considers
the pros and cons of different ways of formulating H1 is included at
the web site.
Under both H2 and H3, there are fewer parameters than independent observations. Thus, there is more than one set of possible solutions, and the maximum-likelihood estimates are the minimum-variance, unbiased set. The estimates under the three hypotheses, and the G-test comparisons, are shown graphically in Fig 5. Under H1, we estimate the nondisjunction rates for each cross separately. Under H2, we obtain the maximum-likelihood estimate of a single nondisjunction rate for all of the crosses. Under H3, we obtain the maximum-likelihood estimates of the slope and intercept for correlated behavior of nondisjunction rate and rDNA exchange rate. In addition, Fig 5 shows the results that are obtained from conventional regression analysis that uses the frequencies of rDNA crossovers and nondisjunctional offspring rather than the actual progeny counts.
|
Likelihood and regression analyses give slightly different estimates of the slope and intercept. Indeed, with regression analysis there are two equally sensible lines of least-squares fit, with the best estimate of the underlying parameters somewhere in between. Regression analysis assumes that the values of one variable, the independent variable, are chosen by the experimenter and are not subject to sampling error. That is not in fact true in this kind of experiment, where both variables are actually determined by the data. Unless we have reason to believe that one parameter is known with greater precision than the other, either can be used as the independent variable. Maximum likelihood, in contrast, gives a single solution that takes account of the effects of sampling variation on both variables.
In neither analysis was the intercept constrained to pass through the origin, but the maximum-likelihood estimate of the intercept is 0 and the intercepts of both regression lines are not significantly different from 0. The statistics, however, are quite different. First, the maximum-likelihood method allows us to isolate a single variable and test whether it shows significant experimental variation in the first place; this cannot be parsed out with regression analysis. Second, the method of maximum likelihood provides a far more powerful test of whether the correlation is significant. In this instance, the regression analysis points to a significant correlation, but only at the 0.025 level; the G test indicates that it is actually very highly significant indeed. In other words, regression analysis, by using frequencies rather than the observed numbers, has thrown away a lot of information. Third, the likelihood analysis provides a direct test of whether the correlation adequately explains the experimental variation. Here, the unexplained variation is not only small, it is statistically insignificant. Regression analysis also provides a measure, if not a direct test, of sufficiency. As long as the intercept is calculated rather than forced through the origin, R2 is the fraction of the variance that is explained by the correlation. Here, with less than half of the variance explained by the (albeit significant) correlation, regression analysis suggests that a substantial fraction of the experimental variation has not been accounted for, while the likelihood analysis tells us that only an insignificant fraction of the variation remains unexplained. In large measure this vagueness indicated by the regression analysis results from the lack of fit between the experimental design that has two variables subject to sampling errors and the assumption of regression analysis that one variable is error free.
A note is in order at this point about the need for care in defining the space within which MLIKELY.PAS searches for the maximum-likelihood solutions. In general, a slope and intercept can take on any positive or negative values, but allowing unconstrained iteration of the slope and intercept can lead to finding local and/or nonsensical bumps in the likelihood function. It is important to provide hints to the program in the form of constraints on the parameter ranges. Inspection of the data before running the program will generally suffice, and even if one fails to do that in advance, the absurdity of the result at a false maximum is quite evident. For these data, it is clear from inspection that the slope of the correlation must be positive. Given that, it is also evident that the intercept must be less than the maximum-likelihood estimate of the average rate of nondisjunction (H2). As long as either of these hints is provided to the program by setting the lower bound of the slope to zero or the upper bound of the intercept to the value previously found for the average, iteration proceeds quickly to the true maximum. If, however, a negative slope is allowed and an intercept greater than the average is allowed and the initial guess of the intercept is greater than that average, iteration to a local maximum is possible. The conjunction of these errors will be obvious, however. If a negative slope is allowed and the initial guess of the intercept is set greater than the average nondisjunction rate but less than the highest observed rate, the false solution under H3 (correlation) will be identical to the solution under H2 (invariant nondisjunction rate). If a negative slope is allowed and the initial guess of the intercept is set greater than the highest observed nondisjunction rate, the false solution for H3 will be even worse—if plotted, the line will not even remotely approach the data points. Even if inappropriate bounds are set, however, MLIKELY.PAS finds the correct solution as long as the initial guess of the intercept is less than the average nondisjunction rate.
Further examples of the range of problems amenable to this
approach:
The foregoing examples, estimating a parameter in the
presence of nuisance variables and analysis of correlation,
illustrate just two of the many problems in formal genetics that can
be tackled using this approach. The web site, in addition to
simpler, introductory examples, contains additional real-world
examples that illustrate two hypothesis-testing problems that arise
with regularity: (1) testing whether only a subset of parameters
differ between a control and an experiment; and (2) taking account
of sampling variation in control crosses done to evaluate confounding
variables. In outline, those examples are as follows:
Differences in the control crosses must be removed before deciding whether there is an effect in the experimental crosses. A simple, but flawed, approach would be adjusting the numbers in the experiment based on the ratios observed in the control. However, sampling errors are inherent in the control as well as the experiment, but "adjusting" the experimental data based on the controls assumes that the controls are error-free. The preferable approach, used by Hearn et al. and detailed in the example, is to construct a model for these viabilities and interactions and apply it simultaneously to all of the data.
| DISCUSSION |
|---|
Maximum-likelihood analysis of data from crosses:
There
are two themes running through the examples used to illustrate this
approach. The first is the wide applicability of a simple numerical
approximation approach to finding maximum-likelihood solutions. The
second is the insight to be gained from partitioning of variation by
even a primitive application of discrete multivariate analysis. In
the teaching context, the first allows students to focus on the ideas
without getting terribly involved in the mechanics, and the second
forces a clear definition of the experimental design and the
questions to be asked.
In many instances these ideas parallel each other, but that is certainly not always the case. For some problems, such as in the example of testing whether a meiotic mutant affects interference, only a test of a single hypothesis is needed, but finding the maximum-likelihood estimates of the multiple exchange and interference parameters is made easier by use of the computer. There are surely few geneticists who would be comfortable trying to solve a set of 14 simultaneous equations for the partial derivatives of L with respect to eight map distances and six coefficients of coincidence. Numerical analysis makes this kind of problem tractable.
There are also problems for which multiple hypotheses must be
compared, but for which the maximum likelihood is readily found.
For example, R. Morell recently posed the following. He was
studying a human dominant of reduced penetrance for which genotypes
could nevertheless be determined unambiguously by molecular
means, even in many instances to the point of knowing whether
the particular allele segregating was, for example, a frame-shift
or a base substitution. Eyeball perusal of several pedigrees
suggested that penetrance was not constant. There are several
things worth examining in this situation. First, of course, is
the question of whether these are significant differences in
penetrance or merely stochastic variation. If there are significant
differences, one might want to know, for example, whether penetrance
is higher for clearly null alleles than for missense alleles or
whether other loci affect expression of this trait. In other words,
we need to ask, as we would in an analysis of variance were we
following a measured variable rather than numbers of affected and
unaffected individuals, whether there are significant differences in
variation between and within groups. Testing a series of hypotheses
was needed here, but, at the same time, there was no need to turn to
numerical approximation to find the several ln 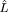 values.
Only one variable was involved, penetrance, and the analytic
solutions were easily found (
values.
Only one variable was involved, penetrance, and the analytic
solutions were easily found (![]()
There are also situations outside of formal genetics in which this approach may be of value. For example, we have recently used this kind of analysis in measurement of ribosomal RNA gene copy number (P. CRAWLEY, unpublished results). Because copy numbers of a large number of genotypes were needed, dot-blot hybridizations, with a single-copy reprobe used to control for loading, were counted using a storage-phosphor screen device. The data were therefore in the form of discrete numbers (photons detected in each of many dots) and maximum-likelihood methods are appropriate for testing for differences among the genotypes. MLIKELY.PAS is not designed for the rather awkward bookkeeping involved in the complex data structure of multiple dots of multiple genotypes on multiple blots with probes that may differ in concentration and specific activity from run to run. Nevertheless, we used it to test the utility of this approach. It does work, and it certainly gives cleaner yes/no judgments of significance than does a chart of error bars.
Regardless of the particular questions being investigated, there are several reasons why this approach to teaching statistics is attractive, at least when a program like MLIKELY.PAS can be used to preempt the need for great mathematical competence:
Of course, this approach, particularly the use of numerical methods for solving a nearly unrestricted optimization problem, has its limitations as well. The MLIKELY.PAS algorithm in which parameters are varied in a fixed order sometimes requires that the user have an idea of reasonable guesses to enter as starting points; it may not recover from entirely unreasonable ones. The possibility of finding local maxima, and of missing the true maximum likelihood by an amount that would affect one's inferences, cannot be ruled out, even though it has been of little practical import in a fairly wide variety of applications. For some hypotheses, the interactions of the parameters can be so complex that iteration to a solution takes longer than is reasonable, even though no more than a few minutes are needed for each of the examples discussed here. Finally, likelihood methods are applicable in many situations other than formal genetics, but MLIKELY.PAS was written specifically with crosses in mind. MLIKELY only works for situations where the observations come in the form of a multinomial sample whose probabilities can all be explicitly stated in terms of the parameters to be estimated.
Some improvements to MLIKELY.PAS can also be envisioned, both for teaching purposes and for research uses. The interface might be improved to allow the user to judge when the precision reached is close enough to cease iteration, but a faster, current-generation computer makes the speed gain entirely trivial. The program could allow an option of varying the parameters in random sequence at each iterative step. At the cost of increased computation time, it would be more likely to recover from absurd initial guesses and less likely to halt at a local peak. A pseudo-Bayesian approach could be implemented for data sets that contain small numbers and many cells where the observed number is zero, by running two successive iterations, the first using the actual data, and the second using a set of numbers biased toward the initial maximum-likelihood expectations. Finally, MLIKELY.PAS' data-handling structures are not well suited to every application for which the maximum-likelihood approach would be an improvement over what one sees in the biological literature. Hopefully, colleagues working in other areas of genetics and molecular biology, or a programmer or two, will be intrigued enough by the power of these methods to adapt them to those situations as well.
| FOOTNOTES |
|---|
1 With apologies to the mathematically oriented, who might
read NCO as N times C times O, common
genetic abbreviations are used to name variables rather
than following mathematical convention. Hence, NCO is to
be read as "noncrossovers." ![]()
2 The procedure outlined here is
decidedly inelegant and provides what is more properly
termed a support interval rather than a conventional
confidence interval, but it requires understanding only
the basic concepts of statistical inference and does not
require understanding variance and covariance nor
knowledge of linear algebra. It is also practical.
![]()
| ACKNOWLEDGMENTS |
|---|
I am grateful to Joe Felsenstein and Richard Lenski for their critical, helpful, and encouraging comments and for their stamina in wading through a manuscript that originally combined the contents of both this report and a paper on meiotic drive. I am especially grateful to Joe Felsenstein for the encouragement and time he gave a then-young graduate student more than 25 years ago when I wrote the first version of the MLIKELY program. I am also grateful to Rob Morell and Ellen Swanson for their criticisms and for the patience they have shown during the long gestation of this article. Finally, I thank the two anonymous reviewers and the corresponding editor who correctly suggested that the article would be more readable with some of the examples and the appendix removed to the website. Research in my laboratory has been supported by National Science Foundation grant MCB-9305846 and by start up funds from the Università di Siena.
| LITERATURE CITED |
|---|
ASHER, J. H., JR., R. W. HARRISON, R. MORELL, M. L. CAREY, and T. B. FRIEDMAN, 1996 Effects of Pax3 modifier genes on craniofacial morphology, pigmentation, and viability: a murine model of Waardenburg syndrome variation. Genomics 34:285-298[Medline].
BISHOP, Y. M. M., S. E. FIENBERG and P. W. HOLLAND, 1975a Discrete Multivariate Analysis: Theory and Practice. MIT Press, Cambridge, MA.
BISHOP, Y. M. M., S. E. FIENBERG and P. W. HOLLAND, 1975b Formal goodness of fit: summary statistics and model selection, pp. 123–175 in Discrete Multivariate Analysis: Theory and Practice. MIT Press, Cambridge, MA.
CROW, J. F., 1993 Felix Bernstein and the first human marker locus. Genetics 133:4-7[Medline].
EDWARDS, A. W. F., 1992 Likelihood (expanded edition). Johns Hopkins University Press, Baltimore.
FISHER, R. A., 1922 On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. Lond. A 222:309-368.
GRIFFITHS, A. J. F., J. H. MILLER, D. T. SUZUKI, R. C. LEWONTIN and W. M. GELBART, 1993 Linkage I: basic eukaryotic chromosome mapping, pp. 132–135 in An Introduction to Genetic Analysis. W. H. Freeman, New York.
GRIFFITHS, A. J. F., W. M. GELBART, J. H. MILLER and R. C. LEWONTIN, 1999 Recombination of genes, pp. 147–151 in Modern Genetic Analysis. W. H. Freeman, New York.
HEARN, M. G., A. HEDRICK, T. A. GRIGLIATTI, and B. T. WAKIMOTO, 1991 The effect of modifiers of position-effect variegation on the variegation of heterochromatic genes of Drosophila melanogaster.. Genetics 128:785-797[Abstract].
HEDGES, S. B., S. KUMAR, K. TAMURA, and M. STONEKING, 1992 Technical comment on human origins and
analysis of mitochondrial DNA sequences. Science 255:737-739
HILLIKER, A. J., G. HARAUZ, A. G. REAUME, M. CLARK, and A. CHOVNICK, 1994 Meiotic gene conversion tract length distribution within the rosy locus of Drosophila melanogaster.. Genetics 137:1019-1026[Abstract].
KASTENBAUM, M. A., 1958 Estimation of relative frequencies of four sperm types in Drosophila melanogaster.. Biometrics 14:223-228.
KING, J. S. and R. K. MORTIMER, 1991 A mathematical model of interference for use in constructing linkage maps from tetrad data. Genetics 129:597-601[Abstract].
LYCKEGAARD, E. M. and A. G. CLARK, 1991 Evolution of ribosomal RNA gene copy number on the sex chromosomes of Drosophila melanogaster.. Mol. Biol. Evol. 8:458-474[Abstract].
MCPEECK, M. S. and T. P. SPEED, 1995 Modelling interference in genetic recombination. Genetics 139:1031-1044[Abstract].
MORELL, R., T. B. FRIEDMAN, J. H. ASHER, and L. G. ROBBINS, 1997 The incidence of deafness is non-randomly distributed among families segregating for Waardenburg syndrome Type 1 (WS1). J. Med. Genet. 34:447-452[Abstract].
MORTON, N. E., 1955 Sequential tests for the detection of linkage. Am. J. Hum. Genet. 7:277-318[Medline].
MORTON, N. E., 1995 LODs past and present. Genetics 140:7-12[Medline].
PALUMBO, G., S. BONACCORSI, L. G. ROBBINS, and S. PIMPINELLI, 1994 Genetic analysis of Stellate elements of Drosophila melanogaster.. Genetics 138:1181-1197[Abstract].
RASOOLY, R. S. and L. G. ROBBINS, 1991 Rex and a suppressor of Rex are repeated neomorphic loci in the Drosophila melanogaster ribosomal DNA. Genetics 129:119-132[Abstract].
ROBBINS, L. G., 1971 Nonexchange alignment: a meiotic process revealed by a synthetic meiotic mutant of Drosophila melanogaster.. Mol. Gen. Genet. 110:144-165[Medline].
ROBBINS, L. G., 1977
The meiotic effect of a deficiency in Drosophila melanogaster with a
model for the effects of enzyme deficiency on recombination. Genetics
87:655-684
ROBBINS, L. G., 1981
Genetically induced mitotic exchange in the heterochromatin of Drosophila
melanogaster.. Genetics 99:443-459
ROBBINS, L. G., 1999
Are unpaired chromosomes spermicidal? A maximum likelihood analysis of
segregation and meiotic drive in ribosomal-DNA deficient Drosophila
melanogaster males. Genetics 151:251-262
SANDLER, L. and M. A. KASTENBAUM, 1958 A note on the frequency distribution of
tetrads by rank in Drosophila melanogaster.. Genetics
43:215-222
SANDLER, L., D. LINDSLEY, B. NICOLETTI, and G. TRIPPA, 1968 Mutants affecting meiosis in natural
populations of Drosophila melanogaster.. Genetics
60:525-558
SNOW, R., 1979 Maximum
likelihood estimation of linkage and interference from tetrad data. Genetics
92:231-245
TEMPLETON, A. R., 1992 Technical comment on human origins and analysis of mitochondrial DNA sequences. Science 255:737.
TERWILLIGER, J. D., 1994 Handbook of Human Genetic Linkage. Johns Hopkins University Press, Baltimore.
WEIR, B. S., 1994 The effects of inbreeding on forensic calculations. Annu. Rev. Genet. 28:597-621[Medline].
WEIR, B. S., 1995 DNA statistics in the Simpson matter. Nat. Genet. 11:365-368[Medline].
ZHAO, H. Y., M. S. MCPEECK, and T. P. SPEED, 1995a Statistical-analysis of chromatid interference. Genetics 139:1057-1065[Abstract].
ZHAO, H. Y., T. P. SPEED, and M. S. MCPEECK, 1995b Statistical-analysis of crossover interference using the chi-square model. Genetics 139:1045-1056[Abstract].
This article has been cited by other articles:
 |
M. Boschi, M. Belloni, and L. G. Robbins Genetic Evidence That Nonhomologous Disjunction and Meiotic Drive Are Properties of Wild-Type Drosophila melanogaster Male Meiosis Genetics, January 1, 2006; 172(1): 305 - 316. [Abstract] [Full Text] [PDF] |
||||
|
| |||||
 |
M. Belloni, P. Tritto, M. P. Bozzetti, G. Palumbo, and L. G. Robbins Does Stellate Cause Meiotic Drive in Drosophila melanogaster? Genetics, August 1, 2002; 161(4): 1551 - 1559. [Abstract] [Full Text] [PDF] |
||||
|
| |||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| HOME | HELP | FEEDBACK | SUBSCRIPTIONS | ARCHIVE | SEARCH | TABLE OF CONTENTS |